Clustering 이란 비감독학습중에 하나로 비슷한 패턴을 가진 Cluster , 즉 군집으로 샘플들을 묶는 것이라고 할 수 있습니다.
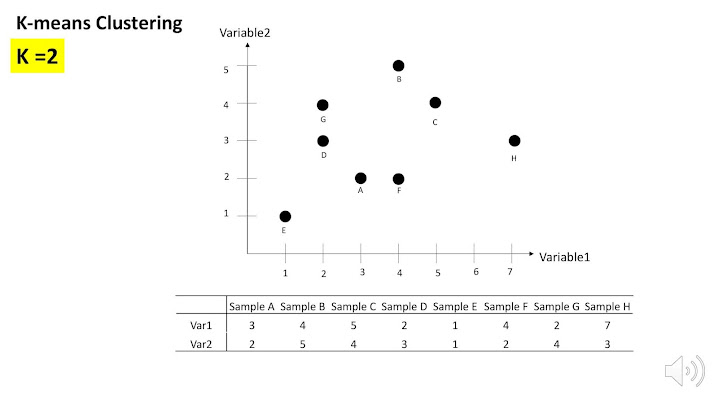
지금 보여지는 것과같은 데이터에서는 , 각각의 검은 점이 샘플입니다. 이 샘플들을 두 군집으로 나누라고 한다면 어떻게 나누실 껀가요? 가장 직관적으로 눈으로 봤을 때
이와같이 두 그룹으로 나누는 것을 생각할 수 있습니다.
그렇다면 이렇게 우리 뇌에서 클러스터링을 하는것이 컴퓨터에서는 어떻게 알고리즘으로 구현되어있는지 쉬운 예제를 통해서 확인을 해보도록 하겠습니다.
아래와 같은 테이블을 보면 샘플 A 부터 H 까지 총 8개의 샘플이 있는 것을 볼수 있고 각각의 샘플은 두개의 변수 즉 variable, 머신러닝에서는 feature 라고 부르는 항복이 두개가 있습니다.
예를들어서 변수로는 키, 몸무게 이런 라벨들이 될 수 있습니다.
이 데이터를 간단하게 그림으로 이렇게 확인해 볼수 가 있습니다.
가장 먼저, k 를 몇으로 할것인지 정해야합니다. K는 군집의 숫자로 해당 데이터를 몇개의 군집으로 묶을 것인지를 의미합니다. 여기에서는 예로 k 를 2로 설정해 보겠습니다.
그 후 해야할 일은 센트로이드를 정하는 것입니다. 센트로이드는 각각 군집에서 중앙에 있는 값입니다. 그런데 사실 컴퓨터가 이렇게 데이터만 읽어서는 어떻게 군집으로 나뉘는게 제일 좋을지도 모르는데, 하물며 어디가 중앙인지 알수가 없죠?
그래서 랜덤으로 두 점을 센트로이드로 정하게 됩니다.
이 예제에서는 그냥 랜덤으로 샘플에이가 첫번째 센트로이드 샘플 비가 두번째 센트로이드로 정하도록 하겠습니다.
자 그렇다면 일단은 각각의 센트로이드들이 군집의 중앙에 있다는 가정으로, 클러스터링을 실행해 보도록합니다. 그렇다면 각각의 센트로이드에 가까운 점들을 묶어야 하니깐 거리를 알아야겠죠.?
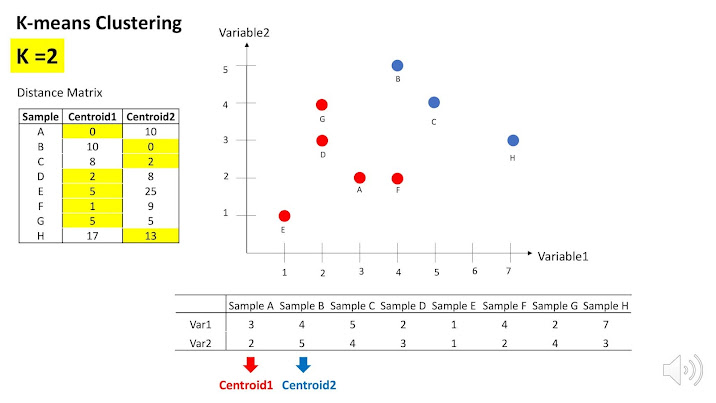
먼저 센트로이드 1으로 보면
센트로이드1으로부터 점들이 떨어져 있는 거리를 이렇게 실선으로 표시했습니다.
이거리를 구할려면 여러 방법이 있는데요, 가장 많이 이용되는 방법으로 유클리디안 거리를 이용할수 있습니다.
유클리디안 거리는 예를들어서 센트로이드1 부터 씨까지의 거리를 계산한다고 했을때 좌표값을 이와같이 나타낼 수 있고,
엑스투 마이너스 엑스 원을 제곱한 값과 와이투 마이너스 와이원을 제곱한 공식으로 계산하여 구할 수있다.
그렇다면 이렇게 실제 값을 다 계산해서 왼쪽 표와 같이 나타낼 수 있다.
그렇다면 센트로이드 1과 가까운 샘플들은 에이, 디, 이, 에프, 쥐 가 있는데 이들이 클러스터 1이 되는것이다.
마찬가지로 센트로이투 와 가까웠던 샘플 비, 씨, 에이치는 클러스터 2에 속하게 된다.
그렇다면 이렇게 클러스터링된것이 최선이라고 할수있을까?
답은 그렇지 않다 이다! 왜냐하면 아까는 랜덤 포인트를 센트로이드로 잡았기 때문에, 사실 이 클러스터가 최선이라는 확신이 없다. 그래서 아까 햇던 과정을 반복할 것인데,
그래도 이번에는 임의의 클러스터를 이렇게 구축해놓았기 떄문에 더 수월해 진다.
이때는 계산은 각 클러스터에 속하는 샘플들의 평균값으로 해주면 된다.
즉 이를 도식화해서 살펴보면 먼저 센트로이들을 설정하고, 센트로이드와 샘플들 사이의 디스턴스 매트릭스를 구축해서 클러스터링을 하고 이 정보를 기반으로 다시 센트로이드를 설정하는 식이다.
이때 클러스터에 변화가 없어지면 과정을 스탑하면 된다.
