1) 왈드 검정
2) 가능도비
3) 스코어 검정
이 있다. 이중, 여기서는 왈드통계량의 개념을 정리해보도록 한다.
왈드 통계량(wald statistic) ? 최대 가능도 추정값을 대입하여 구한 표준오차를 사용하는 통계량.
그러면 먼저 최대가능도(Maximum likelihood)에대해 알아보자!
최대 가능도 추정은 미지의 모수값들을 표본을 이용해 추정하는 방법중 하나이다. 즉, 모수의 함수(최대가능도함수)를 만들고 확률을 최대로 만드는 모수값을 찾는것이다!
만약에 동전을 10번 던졌을때, 앞면이 6번 나왔다고 했을때, 앞면이 나올 확률인 모수 π 를 구해보자.
연속된 10번(동전던지기)의 독립적인 시행이 확률 π 를 가지는 이항분포를 가짐으로 X ~ B(10 ,π)와 같이 표현할 수 있다.
이때, 10번 동전을 던젔을때 6번 앞면이 관찰되었다고 했으므로,
P(6) = [10!/(6!)(4!)]π^6(1-π)^4 이다.
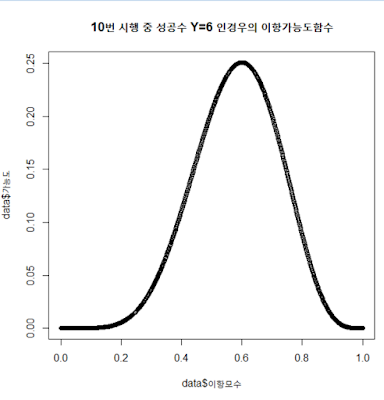
그러면 여기서!! X축을 π 로 놓고 ( 범위는 0부터 1까지). Y축을 P(6)으로 하여 함수 그래프를 그려보자. R로 데이터를 생성하여 다음과 같은 그래프를 그릴 수 있다.
이 함수에서 가능도를 최대로 만드는 모수값,
즉 최대가능도 추정량 (maximum likelihood estimator)은 0.6이다!
보통 이항분포 확률질량함수에서는 x 가 성공할 횟수이고 y는 P(x)로 나타내진다.
성공확률 p 를 알고 있는 상태에서 관찰된 성공 횟수(x)가 변화함에 따라 성공횟수의 확률이 어떻게 변화하는지를 본 것이다.
하지만 위의 MLE에서는 성공확률 p를 미지의 모수로 표현하여 가능도 함수를 만들었다.
그렇다면, 다시 왈드 통계량으로 돌아와보자! 왈드 통계량은 최대 가능도 추정값을 대입하여 구한 표준오차를 사용하는 통계량이다. 이를 z 검정통계량과 연관시켜서 생각해보자.
이때, 표준오차에 최대가능도 추정값을 대입하여 구한 표준오차를 사용하는 것을 말한다.
위의 예에서 최대가능도 추정량 π는 0.6이었다! 그럼 π는 0.6일때 이항분포의 분산은 n*π*(1-π)이므로 10*0.6*0.4이다. 이 분산값을 이용하여 z 검정을 수행하는 것이 왈드 검정인 것이다!!
 과 최대 가능도 추정값 / 스코어검정){kind=link}